Интересно устроено человеческое мышление. На протяжении тысячелетий люди увлекались составлением и исследованием магических квадратов, причем наряду с рядовыми любителями головоломок этим занимались великие умы математической науки. Усложнение задачи шло в направлении увеличения порядка квадрата и расширения накладываемых условий. Появились квадраты симметрические, совершенные или дьявольские, двойные и тройные, но за квадратные рамки никто никак не мог вырваться. Только в начале XX века возник вопрос: почему только квадрат, а не шестиугольник, например?

В 1910 году Клиффорд У. Адаме принялся за поиски магического шестиугольника. Задача формулируется так: можно ли натуральные числа от 1 до n расставить в n ячейках шестиугольника так, чтобы суммы всех чисел в каждом ряду в трех направлениях были бы равны между собой? Наименьший шестиугольник, имеющий более одной ячейки, состоит из семи ячеек.

Шестиугольник третьего порядка состоит из 19 ячеек и имеет по пять рядов в трех направ- лениях. Магическая сумма должна быть равна (1+2+...+19)/5=190/5=38. Но возможность условно вычислить предполагаемую магическую сумму ещё не является доказательством того, что магический шестиугольник третьего порядка существует, его еще построить нужно!

Клиффорд Адаме занимался решением этой задачи в свободное время на протяжении 47 лет и, наконец, решил ее. Вот пример завидного упорства в достижении поставленной цели! Потом лист с записью решения куда-то потерялся и 5 лет он пытался воспроизвести решение ещё раз, пока не отыскал потерянную бумажку. Адаме отослал решение известному популяризатору математики Мартину Гарднеру, а тот передал его для анализа специалисту по комбинаторным задачам Чарльзу Триггу. Тригг доказал, что не существует более ни одного магического шестиугольника любого порядка, т.е. это решение уникально. Есть аналогия с магическими квадратами: второго порядка не существует, а третьего порядка только единственный экземпляр, если не считать симметричные отображения. Но дальше аналогия закончилась, квадратов с увеличением порядка все больше и больше, а шестиугольников кроме одного нет вообще, хоть как увеличивай порядок. Независимо от Адамса в 1958 году такой же шестиугольник опубликовал в «Математической газете» Том Винерс.

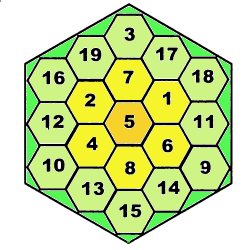
Доказательство невозможности существования магического шестиугольника выше третьего порядка Тригг начал с вывода формулы магической суммы S для шестиугольника 7-го порядка. Для вывода этой формулы достаточно знать, как вычисляется сумма членов арифметической прогрессии, и уметь оперировать не конкретными значениями порядка, а абстрактным обобщением в виде n. Итак, вычислим магическую сумму шестиугольника n-го порядка.

Во-первых, выразим через n количество рядов в шестиугольнике, идущих в каком-то одном направлении. Наглядно мы уже убедились, что у шестиугольника 2-го порядка 3 ряда, 3-го порядка - 5 рядов и далее, при увеличении порядка на единицу, количество рядов увеличивается на два. Эта зависимость выражается формулой: количество рядов равно 2n-1.

Во-вторых, подсчитаем количество чисел в шестиугольнике n—го порядка. В первом ряду (и в последнем) n чисел, во втором (и предпоследнем)-n+1 , в третьем (и втором от конца) n+2 ,..., наконец, в среднем, самом длинном, 2n-1. Сложим все эти выражения: 2(n+(n+1)+(n+2)+..Л(2n-2))+2n-1=(Зn-2)(n-1)+(2n-1)=Зn^2-Зn+1 Так как числа начинаются с 1, то количество чисел совпадает с последним числом, т.е. Зn^2-Зn+1 -это и количество чисел, и последнее число в шестиугольнике n-го порядка.

Чтобы найти магическую сумму, остается сложить все числа и поделить на количество рядов в одном направлении. S=[1+(3n^2-3n+l)](3n-3n^l)/[2(2n-l)]=[9(n Затем, используя методы решения диафантовых уравнений, Тригг показал, что это выражение принимает целые значения лишь при n=1 или n=3. Доказательство единственности решения для шестиугольника третьего порядка он провел перебором всех возможных вариантов. Сейчас это можно перепроверить с помощью компьютера, что и было сделано. Перебрав все комбинации чисел, ЭВМ установила единственность магического шестиугольника третьего порядка. Как меняются времена: задача, над которой К. Адаме бился почти полвека, в 1979 году была предложена простым советским школьникам в детском физико-математическом журнале «Квант», как обычная рядовая задача. Пора показать этот исторический и уникальный магический шестиугольник, на случай если вы сами еще не решили эту задачу. Рядом линиями показана симметрия в расположении чисел.

Итак, магический шестиугольник существует, причем в единственном варианте, цель достигнута и одновременно вопрос исчерпан. Что же делать дальше, полюбоваться этим уникумом и всё? Примитивный подход. Фантазии ума ограничений быть не может. Вспомните квадрат без одной клетки. Перенесем эту идею на шестиугольник и снова простор для головоломок: построить магический шестиугольник с одной или несколькими незаполненными ячейками, или же убирая некоторые числа из натурального ряда, составить магический шестиугольник из непоследовательных чисел. Именно так была поставлена задача в журнале «Наука и жизнь» и читатели нашли много решений, причем не только третьего порядка, но и выше. Задачи сгруппированы в конце данной главы, пока же продолжим мыслить в направлении разнообразия форм магических фигур.