Магия чисел.
Магия чисел>>Кросс-суммы>>Числовые квадраты
Теоретическая часть
Наконец, как это употреблять? Вариантов много и они зависят от конкретной ситуации. Кто-то будет решать как кроссворд в газете, вписывая простым карандашом числа и стирая их, если не подходят. Учитель изготовит крупный рисунок и фишки с числами к нему, чтобы можно было решать у демонстрационной магнитной доски. Человек, трепетно относящийся к книгам, перечертит рисунок на тетрадный листок, и будет решать на нем. Я уже упоминал об удобстве использования бочонков от игры лото с готовыми цифрами. Их можно расставлять, передвигать на любой плоской поверхности.
И ещё одно замечание по построению статей. Можно взять пять задач, к каждой придумать длинную и увлекательную литературную историю, дать запоминающееся название и отвести на них несколько страниц книги. Здесь принято иное решение: показать максимум вариантов, не пять, а пятьдесят или больше, но убрать лишние слова - только номер задачи и её условие.
Примечание: при решении головоломок удобно пользоваться бочонками от настольной игры лото, на которых стоят
цифры от 1 до 90. Передвигать бочонки на столе гораздо проще,
чем делать записи на листе бумаги, а потом их стирать
Задачи: Числовые Квадраты
Расставьте числа от 1 до 16 таким образом, чтобы сумма пяти чисел каждого ряда (2-х вертикальных и 2-х горизонтальных) равнялась 41 (или 42, или 43, или 44). |
 |
Расставьте числа от 1 до 9 так, чтобы суммы чисел в вершинах любого квадрата, из шести представленных на рисунке, были равны между собой. |
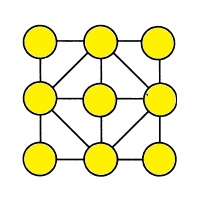 |
|
Подберите 13 натуральных чисел, из них 11 различных, а 2 одинаковых и впишите их так, чтобы сумма трех чисел в каждом ряду вдоль линии равнялась 20. |
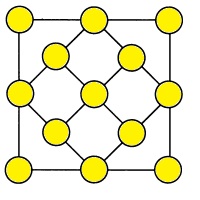 |
Расставьте числа от 1 до 11 так, чтобы сумма трех чисел на каждом из десяти отрезков была одна и та же. |
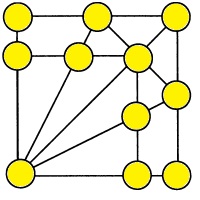 |
|
Расставьте числа от 1 до 16 так, чтобы сумма чисел вдоль контуров всех квадратов была одинаковой и равнялась 68. |
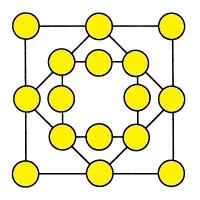 |
Числа от 1 до 12 расставьте в кружках фигуры так, чтобы сумма чисел в вершинах каждого закра-шенного квад-рата равнялась 30. |
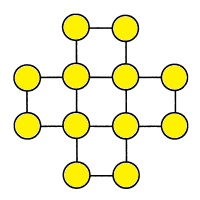 |
|
Расставьте числа от I до 12 так, чтобы сумма чисел в вершинах каждого из пяти квадратов и по четырем прямым была одинаковой. |
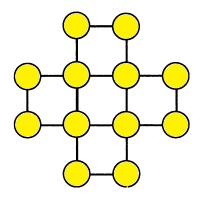 |
Расставьте числа от 1 до 8 так, чтобы сумма чисел в вершинах каждого четырехугольника (2-х квадратов и 4-х трапеций) равнялась 18. |
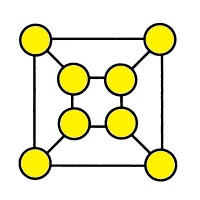 |
|
Расставьте в кружках чис- ла от 1 до 8 так, чтобы сумма чисел в вершинах каждого белого треугольника равнялась 12, а в вершинах серого треу-гольника и квадрата - по 11. |
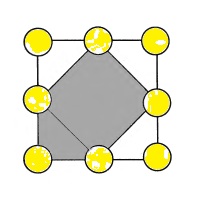 |
В кружочки фигуры расставьте числа от 1 до 13 так, чтобы сумма четырех чисел, распо-ложенных в вершинах всех 11 квадратов, была постоянной. |
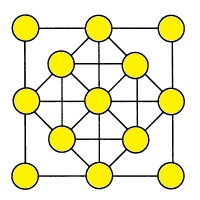 |
|
