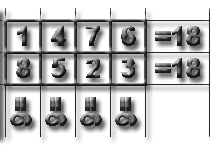Квадрат - это прямоугольник, у которого все стороны равны. А если стороны не равны, то, разбивая прямоугольник на квадратные клетки, получим разное количество клеток в строчке и в столбике. В таком случае невозможно добиться равенства сумм по всем строчкам и столбцам одновременно. Ослабим требования, назовем магическим прямоугольник, у которого суммы чисел по всем строчкам равны между собой и отдельно равны между собой суммы чисел по всем столбцам, т.е. у прямоугольника будет две магические суммы, одна для строчек, другая для столбцов.

Назвать - назвали, а можно ли его построить?

Продолжим поиск. Прямоугольник 2x4 должен содержать числа от 1 до 8. Сумма 1+2+...+8=36, делится и на количество строчек, и на количество столбиков. Разбив числа на пары с одинаковой суммой, легко получаем магический прямоугольник 2x4. Можно сделать первые выводы. Необходимое условие его существования - сумма расставляемых чисел должна делиться и на количество строчек, и на количество столбиков. Кроме того, отношение сумм по строчкам и по столбикам равно отношению количества столбиков к количеству строчек. Перейдем к размеру 3x4. 5=1 +2+...+12=78 не делится на 4, пролетаем не задерживаясь к размеру 3x5. 1+2+...+15=120, делится и на 3, и на 5, прямоугольник возможен.

Ставим задачу в общем виде. Числа от 1 до пк требуется разместить в прямоугольнике из n строк и k столбцов так, чтобы образовались две магические суммы: S1=(1+nk)k/2 для каждой строчки и S2=(l+nk)n/2 для каждого столбца, тогда этот прямоугольник будем называть магическим. Необходимое условие для построения такого прямоугольника выяснено, существование доказано двумя примерами, дальнейшее в ваших руках.