Магия чисел>>Кросс-суммы>>Числовые окружности

Теоретическая часть

Числа и фигуры могут объединиться, например, в такую композицию.Девять чисел натурального ряда расставлены в клетках квадрата. Можно ли сразу сказать, что это красиво? Вряд ли. Красота здесь не внешняя, а содержательная, внутренняя. Чтобы ее понять требуется напряжение мысли, нужно посчитать суммы трех чисел в каждой строчке, в каждом столбце и по каждой из двух диагоналей. Оказывается, сумма во всех восьми случаях одна и та же, равная 15.

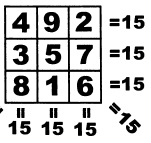Выходит в огромном количестве различных расположений девяти чисел в клетках квадрата можно найти такое удивительное по своему содержанию. От хаоса различных, ничем не примеча- тельных вариантов расположения - к своеобразному и редкому упорядочению. История происхождения подобных квадратов уходит в глубь тысячелетней истории человечества. Естественно, в те древние времена, когда даже отдельным числам приписывались магические свойства, подобные числовые построения не могли назвать иначе как волшебные или магические квадраты. К магическим квадратам вернемся отдельно, а пока рассмотрим более простые, но и более разнообразные расположения чисел с постоянными суммами.

Именно в этой области существует большое количество занимательных задач простых по условию и полезных для ума. Для пересекающихся рядов чисел с одинаковыми суммами отечественный математик и популяризатор науки Борис Анастасьевич Кордемский ввел определение кросс-суммы, по аналогии с кроссвордами (от английского cross - пересекаться,скрещиваться). Таким образом, кросс-суммы - это пересекающиеся ряды чисел с одинаковыми суммами. Словосочетание немного неблагозвучное из-за трех букв «с», идущих подряд. Можно было бы назвать их по-русски: числовые пересечения с одинаковыми суммами, но получается более громоздко. Кроме того, нужно отдать долг вежливости по отношению к мэтру отечественной занимательной математики, автору «Математической смекалки», на книгах которого воспитывалось наше поколение. Начнем с простейшего расположения чисел в одну строчку и один столбец с пересечением:

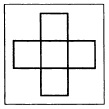
Можно ли расставить числа от 1 до 5 так, чтобы сумма трех чисел в строчке и трех чисел в столбце была одна и та же? Ответ дается в приведенной схеме:

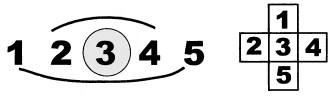
Число 3 в центр, а по краям равноудаленные от центра пары чисел. Это не единственное решение. Сумма 1+2+3+4+5=15, нечетная. Число, стоящее на пересечении, входит как в сумму чисел строки, так и в сумму чисел столбца, и мы должны приба- вить его к 15 и, поделив на два, вычислим кросс-сумму. Значит, число на пересечении обязательно нечетное, но это может быть 1, 3, 5. Отсюда получим другие решения, с суммой равной 8 или 10. Ещё возможны перестановки крайних чисел, не влияющие на сумму, но дающие дополнительные решения. Убеждаемся, что вариант с одним пересечением достаточно легкий и допускает несколько решений с различными кросс- суммами.

Задачи: Числовые окружности

Расставьте числа от 1 до 9 в кружочки фигуры так, чтобы сумма трех цифр по каждой прямой составляла 15. Показать ответ Расставьте десять последовательных натуральных чисел в кружочки фигуры так, чтобы сумма любых трех чисел по каждой прямой, составляла 42. Показать ответ Расставьте числа от 1 до 19 в кружочки фигуры так, чтобы сумма любых трех чисел на одной прямой равнялась 30. Показать ответ Расставьте числа от 1 до 8 так, чтобы суммы чисел по прямым и окружностям были одинаковыми. Показать ответ Расставьте числа от 1 до 10 в маленькие кружочки так, чтобы суммы чисел в четырех больших кругах были равными. Показать ответ Расставьте 9 натуральных последовательных чисел так, чтобы равнялись 60 суммы по 4 малым и одной большой окружности, а также в вершинах центрального квадрата. Показать ответ Расставьте числа от 1 до 16 так, чтобы суммы по 4-м радиусам и 4-м окружностям равнялись 34. Показать ответ Расставьте числа от 1 до 8 так, чтобы сумма чисел на каждой окружности была одной и той же. Показать ответ Расставьте числа от 1 до 25 так, чтобы сумма чисел по пяти радиусам и по пяти окружностям равнялась 65. Показать ответ Расставьте числа от 1 до 6 в маленькие кружочки так, чтобы сумма четырёх чисел на любой окружности равнялась 14. Показать ответ