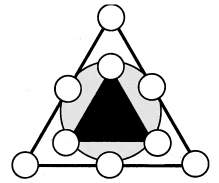
Расставьте числа от 1 до 9 так, чтобы сумма чисел в вершинах малого треугольника равнялась квадрату одного из этих чисел, сумма чисел по окружности - кубу того же числа, а сумма чисел по контуру большого треугольника - сумме квадрата и куба этого числа.

Расставьте все десять цифр 0,1,2, 3,4,5,6,7,8,9 в таком порядке, чтобы получившееся число делилось на все числа от 2 до 18.

Составьте из всех десяти цифр от 0 до 9 такое десятизначное число, что число из двух его первых цифр делится на 2, из трех первых цифр делится на 3 и т. д. до того, что само число делится на 10.

Заполните пустые клетки так, чтобы сумма чисел, стоящих в любых трех подряд идущих клетках, равнялась 15.

Расставьте некоторые числа в пустые клетки так, чтобы сумма любых трех соседних чисел была одна и та же, а сумма всех чисел равнялась 200.

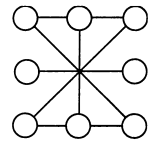
Расставьте цифры от 1 до 8 так, чтобы в горизонтальных рядах получились числа, являющиеся квадратами, а сумма чисел, расположенных в центрально-симметричных кружках была одна и та же.

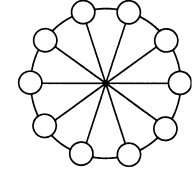
На концах пяти диаметров расположите числа от 1 до 10 так, чтобы сумма любых двух соседних чисел равнялась сумме двух противоположных им чисел.

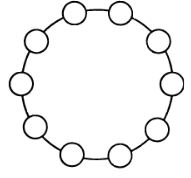
Можно ли все 10 цифр от 0 до 9 расставить по окружности так, чтобы сумма любых трех из них, идущих подряд, не превышала: а) 13, б) 14, в) 15?

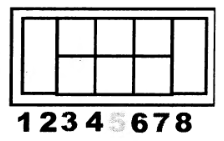
Расставьте числа от 1 до 8 в клетках прямоугольника так, чтобы любые два последовательных числа не были соседями по горизонтали, вертикали или диагонали.

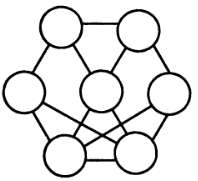
Расставьте числа от 1 до 7 так, чтобы в любом из двух соседних (соединенных прямой) кружках находились числа, не являющиеся «соседями» в натуральном ряду чисел.

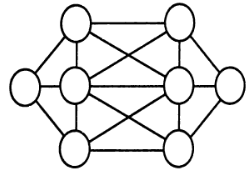
Расставьте числа от 1 до 8 так, чтобы числа в кружочках, соединенных отрезками, отличались не меньше чем на 2.

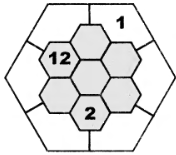
Расставьте числа от 1 до 13 (некоторые из них уже стоят на своих местах) в клетки фигуры так, чтобы в клетках, имеющих общую сторону, числа отличались, по крайней мере, на 3.

Расставьте числа от 1 до 13 (некоторые из них уже стоят на своих местах) в клетки фигуры так, чтобы в клетках, имеющих общую сторону, числа отличались, по крайней мере, на 3.

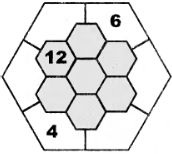Расставьте числа от 1 до 13 (некоторые из них уже стоят на своих местах) в клетки фигуры так, чтобы в клетках, имеющих общую сторону, числа отличались, по крайней мере, на 3.

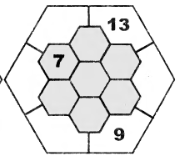В кружках фигуры расставлены числа от 1 до 18. Докажите, что найдется отрезок, на концах которого стоят числа с разностью, большей трех.

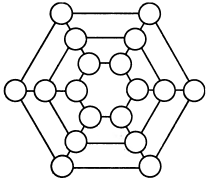В 25 клето-чек нужно впи-сать как можно больше различ-ных чисел от 1 до 25, соблю-дая при этом одно условие: разница между числами в квадратах, соединенных линиями, дол-жна быть не менее 10. На чемпионате мира по голо-воломкам уда-лось вписать все числа, кроме тройки. А как получит-ся у вас?

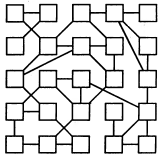Расставьте числа от 1 до 10 так, чтобы сумма чисел в любых двух соседних кружках не делилась ни на 3, ни на 5, ни на 7.

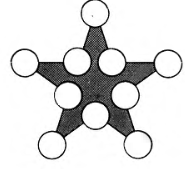Можно ли в кружках звезды расставить десять натуральных различных чисел так, чтобы суммы четырех чисел вдоль каждой из пяти прямых были нечетными?

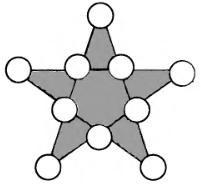Заполните прямоугольник цифрами так, чтобы в каждом горизонтальном ряду стояло четырехзначное число, делящееся на 92, а в каждом вертикальном ряду - трехзначное число, также делящееся на 92.

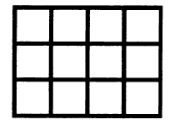Расставьте цифры от 1 до 9 так, чтобы три, образовавшихся в горизонтальных рядах, числа были точными квадратами.

Заполните квадрат цифрами так, чтобы по краям и диагоналям в любом направлении читались квадраты натуральных чисел (цифры могут повторяться).

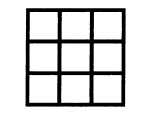Расставьте цифры от 1 до 9 так, чтобы в 3-х горизонтальных рядах и каждом из 5-ти вертикальных столбцов получались различные квадраты натуральных чисел. Некоторые цифры могут повторяться.

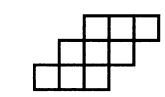Расставьте числа от 1 до 9 так, чтобы пять чисел, запись которых получается по горизонтальным прямым, были бы квадратами целых чисел.

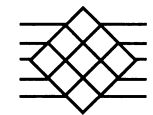Расставьте цифры от 0 до 9 так, чтобы по горизонталям получилось четыре квадрата натуральных чисел. Сколько решений имеет эта задача?

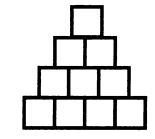Запишите в клетках фигуры, изображенной на рисунке, цифры от 1 до 9 с повторением так, чтобы во всех вертикальных и горизонтальных полосках из трех клеток стояли различные трехзначные числа, являющиеся полными квадратами.

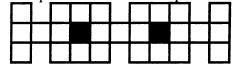Расставьте цифры 1, 3, 5, 7 и 9 так, чтобы произведение двузначного числа, образованного двумя цифрами, на число, образованное двумя другими цифрами, минус последняя цифра равнялось числу, составленному из повторений одной и той же цифры.

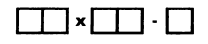Два сомножителя составлены из всех цифр от 1 до 9 так, что их произведение - целое число. Какие два числа перемножаются?

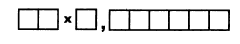Впишите в клетки цифры от 1 до 9, каждую по одному разу, так, чтобы произведение оказалось наибольшим.

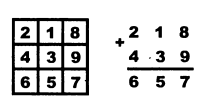
Из девяти цифр от 1 до 9 составьте квадрат таким образом, чтобы трехзначные числа, стоящие в первой и второй строках, в сумме давали третью строку. Один из примеров решения показан на рисунке, но он не единственный.