Игральные кости

На каком-то этапе развития из атрибута гадания кости превратились в инструмент азартных игр. Для этого неизвестные мастера стали изготавливать игральные кости из дерева, камня, из бивня слона и т.д. История убедительно свидетельствует, что азартные игры с игральными костями появились задолго до строительства пирамиды Хеопса, т.е. за 3000 лет до нашей эры они уже были. В различных музеях мира хранятся образцы древнеегипетских, древнегреческих, римских, китайских игровых костей. Чаще всего они имели форму кубика с выемками на гранях, обозначающими числа от 1 до 6. Хотя есть образцы в виде других многогранников: прямой призмы с различным количеством боковых поверхностей; кубооктаэдра с 14 гранями; в виде призматического волчка и другие. До наших дней не вышли из употребления игральные кости в виде кубика, остальные хранятся как музейные экспонаты. Преимущества кубической формы игральной кости имеют вполне резонные объяснения:

- только правильный многогранник обеспечивает полное равноправие всех граней;

- из пяти существующих в природе правильных многогран- ников куб легче всего изготовить;

- он перекатывается легко, но не слишком. Тетраэдр перекатывается труднее, а, додекаэдр и икосаэдр настолько близки по своей форме к шару, что быстро укатываются.

 

Западный стандарт требует, чтобы сумма чисел на противоположных гранях равнялась семи: 6-1,5-2, 4-3. Существует только два различных способа нумерации костей, причем один из них является зеркальным отображением другого и, более того, все современные игральные кости нумеруются одинаково.

Если держать кубик так, чтобы были видны три числа 1, 2 и 3, то цифры будут расположены в порядке, обратном движению часовой стрелки.

Почему эти игры были именно азартными, то есть предполагали какие-то ставки в игре, деньги или вещи, которые можно было выиграть или проиграть?

Наверное, потому, что при бросании игральной кости не требовалось думать - подбросил и отдался на волю случая. Если не подсластить это действие возможностью сорвать куш, то другого смысла в бестолковом бросании костей попросту нет. В отличие, например, от шахмат, где сам длительный процесс борьбы умов приносит удовлетворение, люди с удовольствием играют без дополнительных стимулов, и то уже не всегда.

Азартные игры с игральными костями, как это ни странно звучит, принесли пользу науке, послужили толчком к развитию комбинаторики и математической теории вероятностей. Эта тео- рия начиналась с исследования различных видов азартных игр, с целью установления закономерностей в случайных событиях, определения вероятности выигрыша или проигрыша. В борьбе со случайностью эти знания ничего не изменяют, но могут предостеречь, дать возможность реально оценить свои шансы на выигрыш, а уж тогда решать: ввязываться в игру или благоразумно отказаться. Знание шахматных дебютов, шахматной теории, будет полезно в самой игре и может привести к победе, а знание теории вероятностей ни на игральную кость, ни на шарик в американской рулетке не подействует, вы останетесь наедине со случайностью. Хотя интересно все-таки знать, что и случайность имеет свои закономерности.

Игры в кости, могут проходить с различным количеством бросаемых одновременно костей. Начнем с одной кости.

 

Игра примитивная

 

Примитивная игра с одной костью состоит в том, что игроки поочередно бросают её и побеждает тот, у кого выпадет большее число очков. При равенстве очков, игроки повторяют бросок. Вряд ли кого заинтересует такая игра, поэтому такая процедура используется чаще не для самой игры, а при жеребьевке в каких-то других играх или делах.

Но даже этот простой вариант позволяет нам потренировать свое логическое мышление. В истории развития математического аппарата азартных игр было много случаев неправильной логики, которые приводили к неверным результатам. Рассмотрим подобный пример.

При подбрасывании одного игрального кубика вероятность появления единицы равна 1/6. При втором подбрасывании - тоже. Значит, если провести два броска, то вероятность появиться единице хотя бы один раз (при первом броске или при втором) равна 1/6+1/6=1/3. Рассуждая аналогично, получается, что для шести бросков вероятность выпадения 1 хотя бы один раз из шести равна единице (1/6-6=1), т.е. является достоверным событием. Мы можем применить эти рассуждения к любому из чисел от 1 до 6, и сделать вывод, что каждое число при проведении шести бросков, обязательно выпадет. С другой стороны опыт подсказывает нам, что это не так. Бросьте кость шесть раз и вряд ли, каждое из возможных чисел, выпадет ровно по разу. В чем ошибочность рассуждений? Высказывание: «единица выпала хотя бы один раз при двух бросках» на самом деле распадается на несколько различных событий:

• выпала в первый раз и не выпала во второй (1/6-5/6) или

• не выпала в первый раз и выпала во второй (5/6-1/6) или

• выпала в первый раз и во второй тоже (1/6-1/6).

Соответствующая вероятность подсчитывается как 5/36+5/36+1/36-11/36, что немножечко меньше чем 1/3. Для шести бросков подсчет лучше начать по-другому. Вероятность того, что 1 не выпала при одном броске 5/6, при двух бросках 5/6-5/6, соответственно вероятность, что 1 не выпала при шести бросках равна(5/6)6. А значит вероятность, что она выпала хотя бы раз в шести бросках равна 1-(5/6)6 = 0,66510.

Игра с дополнением

Первый игрок бросает кость и складывает число, выпавшее на верхней грани, с любым числом на одной из четырех боковых граней. Его соперник складывает все остальные числа на трех боковых гранях. Нижняя грань в расчеты не принимается. Затем второй игрок бросает кость, и они проводят аналогичные подсчеты. Выигрывает тот игрок, у которого после бросков обоих игроков, будет больше итоговая сумма. К слепому случаю добавилась маленькая возможность для выбора самим игроком одного из боковых чисел, хотя, что там выбирать - нужно брать наибольшее. К тому же еще в уме числа сложить придется, получается, что добавили мышление.

 

Перевороты кости

Для этой игры опять-таки нужна одна игральная кость. Первый игрок называет любое число от 1 до 6, а второй бросает кость. Затем они по очереди переворачивают кость через её ребро в любую сторону на четверть полного оборота. К числу очков, названных первым игроком, прибавляется число очков, выпавших на верхней грани после бросания кости и после каждого её поворота. Выигрывает тот из игроков, которому удается при очередном повороте достичь суммы 25 очков или вынудить противника при следующем повороте превзойти 25 очков.

Всего на третьем шаге, оставаясь с одной игральной костью, мы пришли к необходимости серьезно думать.

Какое число должен назвать первый игрок, чтобы выиграть с наибольшими шансами?

Игры с двумя костями были настолько популярны на протяжении веков, что у них есть свои исторические названия и определенная терминология.

 

Азар

Название игры происходит от арабского выражения «аз-захр» - «игральные кости».

Игрок, выступающий в роли банкомета, ставит против остальных участников, число которых неограничено, на то, что ему удастся с помощью двух костей выбросить одно из следующих чисел: пять, шесть, семь, восемь или девять. Противники, в свою очередь, обязаны уравнять его ставку.

Загаданное банкометом число называется «мейн». Если после его броска выпадает «мейн», то банкомет получает все деньги, поставленные на кон. Такой удачный ход получил название «ник». Если же выпадает какое-то иное число, его называют «чане», то для банкомета еще не все потеряно. Он обязан продолжать бросать кости до тех пор, пока вновь не выбросит «чане» - тогда он выиграл, или выпадет «мейн» - тогда он проиграл и должен выплатить деньги.

В казино имел распространение азар с бросанием трех костей и иными правилами, о нем поговорим позже.

 

Крэпс

Игра «Крэпс» одна из популярнейших в Америке. Изобретена в IX веке черными невольниками с берегов Миссисипи. Игрок бросает две кости и подсчитывает сумму выпавших очков. Он сразу же выигрывает, если эта сумма равна 7 или 11, и проигрывает, если она равна 2, 3, или 12. Всякая другая сумма - это его «пойнт». Если в первый раз выпадает «пойнт», то игрок бросает кости ещё, до тех пор, пока он или выиграет, выбросив свой «пойнт», или проиграет, получив сумму очков, равную 7. Проведем некоторые размышления по поводу бросания двух игровых костей. Для начала посчитаем вероятности для полного числа очков на двух костях. Будем считать, что одна из них белого цвета, а вторая - черная. Это немаловажная деталь в рассуждениях, так как мы должны различать кости, а, следовательно, и такие варианты возможных исходов, как (3,5) и (5,3). Подбрасывание двух костей имеет 36 равновероятных исходов, которые мы обобщили в виде таблицы.

В клетках таблицы указаны получаемые суммы очков. На основе первой таблицы модно просчитать распределения вероятностей получения определенной суммы очков при подбрасывании двух игральных костей. Эти значения оформим таблицей .

 

Здесь нижняя строка обозначает вероятность появления соответствующей суммы очков. Таблица позволяет подсчитать вероятность выигрыша после первого броска

Р(7)+Р(11)=6/36+2/36=8/36=2/9

Вероятность проигрыша после первого броска равна

Р(2)+Р(3)+Р( 12)= 1 /3 6+2/36+1 /36=4/3 6= 1 /9

Таким образом, теория говорит, что вероятность выигрыша при первом броске в 2 раза больше вероятности проигрыша, но еще больше (2/3) составляет вероятность того, что игра не остановится на первом броске, а будет продолжена. Попробуйте сами провести исследование вероятности при первом броске «пойнт» снова его выбросить в дальнейшей игре.

 

Попытай счастья

Это азартная игра с тремя игральными костями. В неё часто играют в игорных домах и во время народных гуляний на ярмарках или карнавалах. На прилавке лежат шесть квадратов, поме- ченных цифрами 1, 2, 3, 4, 5, 6. Игроки делают стандартные одинаковые ставки на один из номеров, после чего подбрасываются три игральные кости. Если номер играющего выпадает на одной, двух или трех костях, то за каждое появление этого номера игроку выплачивается первоначальная ставка, при этом возвращаются и его собственные деньги. Игроки, чей номер не выпал ни разу теряют ставку. Игрок может ставить на несколько номеров одновременно, но каждая ставка рассматривается отдельно.

Игра проста и увлекательна. Только необразованность объясняет то, что ее обошли вниманием наши «лохотронщики», ведь никакого криминала.

Предположим для простоты, что на каждый номер положена единичная ставка. Игра безобидна только в случае, когда все три выпавших номера различны. Тогда, получив на шесть номеров шесть ставок, игорный дом расплачивается этими деньгами с тремя удачливыми игроками, отдавая им три выигранных ставки возвращая три поставленных. В этом случае организаторы игры ничего не имеют, а только перераспределяют деньги между везучими и проигравшими. Так будет всегда, когда выпадают три различных номера, но не всегда будут выпадать все разные номера.

Предположим теперь, что после подбрасывания костей выпало ровно два одинаковых номера. Из шести полученных ставок три отдадут игроку, чей номер выпал дважды (с учетом возвращаемой ставки) и две - игроку, чей номер выпал один раз. Получается, что при таком раскладе одна ставка остается у игорного дома.

Наконец, пусть на всех трех костях выпал один и тот же номер. Тогда один игрок получает четыре ставки, три выигран ных и одну возвращаемую, а игорному дому остаются уже две ставки игроков.

Рассмотрим вероятность этих случаев. Пусть игральные кости различаются по цвету, например, красная, зеленая и синяя. Они могут выпасть 6*6*6 = 216 способами.

Легко просчитать последний случай, когда выпадают три одинаковых номера. Число таких вариантов всего 6, так как красная кость может выпасть любой из 6 граней, а зеленая и синяя только той единственной, которой уже выпала красная кость. Определим, сколькими способами могут выпасть три различных номера. Для красной кости имеется 6 различных вариантов, для зеленой - только 5, потому что номер, выпавший на красной кости, не должен повторяться, аналогично рассуждая, синяя кость может выпасть только одной из 4 граней. Итого 6*5*4 = 120 вариантов.

Отсюда следует, что в 90 случаях выпадают два одинаковых номера (216 - 126 = 90). Вероятность получения ставки игорным домом равна (120/216)*0+(90/216*1+(6/216)*2 = 102/216.

Это означает, что количество единичных ставок игроков, остающихся в игорном доме приблизительно равно половине проведенных игр и никаких потерь. При таком раскладе выгодно работать круглосуточно.

Теперь рассмотрим эту игру с точки зрения игрока. Из 216 равновероятных исходов он выигрывает только в 91 случае и проигрывает в 125. Откуда мы взяли цифру 91? Допустим, игрок поставил на «единицу». Один из 216 исходов - это когда выпадают все три единицы; из 90 случаев с двумя одинаковыми цифрами третья часть включает в себя единицу; из 120 вариантов с тремя различными числами единица входит в половину. Итого: 1+30+60=91.

Эта вероятность существенно отличается от вероятности выигрыша для игорного дома. Хотя цифры 102/216 и 91/216 не очень сильно различаются, но для игорного дома они означают неминуемую прибыль, а для игрока более вероятный проигрыш, чем выигрыш.

Сложнее будут вычисления, если игрокам разрешить делать не фиксированные, а произвольные ставки на различные числа. При таких правилах есть вероятность, что на начальном этапе игорный дом вложит какую-то сумму в игру, когда маленькие ставки проигравших игроков не покрывают большую ставку выигравшего, но если игра длится достаточно долго, то организатор игры может надеяться получить 7,8% от каждого поставленного игроками доллара. Попробуйте вывести эту цифру самостоятельно.

 

Три кости

Сначала каждый игрок называет некоторое число от 3 до 18 . Бросают три кости. Выигрывает тот игрок, у которого сумма выпавших очков равняется числу, названному им перед игрой. Определим шансы игрока в зависимости от названного им числа. Три игральные кости подбрасывают над столом и считают сумму,очков выпавших на верхних гранях. Сколько различных исходов возможно для одного подбрасывания кубиков?

Каждый кубик может показать на верхней грани одно из шести чисел: 1, 2, 3, 4, 5, 6. Комбинируя 6 расположений первого кубика с шестью расположениями второго, получим 6*6=36 вариантов для двух кубиков. Каждое из этих 36 расположений двух кубиков в сочетании с одним из 6 расположений третьего кубика дают 36-6=216 сочетаний по 3 числа. Одинаковы ли вероятности появления у каждой суммы от наименьшей (1-3) до наибольшей (6-3)?

Сравним, например, вероятности получения сумм 9 и 10. На первый взгляд вероятности одинаковы. Три кубика формируют 6 троек чисел, дающих в сумме 9 - (6, 2, 1), (5, 3, 1), (5, 2, 2), (4, 1, 1), (4, 3, 2), (3, 3, 3), и столько же формируют троек чисел с суммой 10 - (6, 3, 1), (6, 2, 2), (5,4, 1), (5, 3,2), (4, 4, 2), (4, 3,3). Чтобы не допустить ошибки в рассуждениях, предположим, что наши кубики окрашены, например, по системе RGB, т. е. красный, зеленый и синий. Тогда первая тройка чисел, дающая сумму 9, фактически распадается на шесть объективно различных вариантов: (6, 2, 1), (6, 1, 2), (2, 1, 6), (2, 6, 1), (1, 2, 6), (1, 6, 2). В этой записи на первом месте стоит число, выпавшее на красном кубике, на втором месте число, выпавшее на зеленом и на третьем - выпавшее на синем кубике. Если в тройке чисел, дающих нужную сумму, два числа одинаковые, то с учетом раскраски получается три различных расклада. Например, - (5, 2, 2), (2, 5, 2),(2, 2, 5).

При трех одинаковых числах, перестановки не создают различающихся случаев и возможен только один вариант. Вот теперь подсчитаем число случаев, дающих сумму 9, с учетом индивидуальности кубиков: 6+6+3+3+6+1=25. Аналогичный подсчет для суммы 10 даст результат: 6+3+6+6+3+3=27. Пусть не намного, но при броске трех игральных костей вероятность появления суммы 10 больше, чем вероятность суммы 9. Таким образом, можно посчитать вероятности появления каждой из возможных сумм от 3 до 18. В итоге все 216 возможных исходов распределятся по своим суммам. Первым, кто правильно провел подобные рассуждения, был знаменитый ученый Галилео Галилей.

 

Азар в три кости

Эта игра распространена в казино и, следовательно, в ней играет казино в лице крупье против игроков, делающих ставки.

 

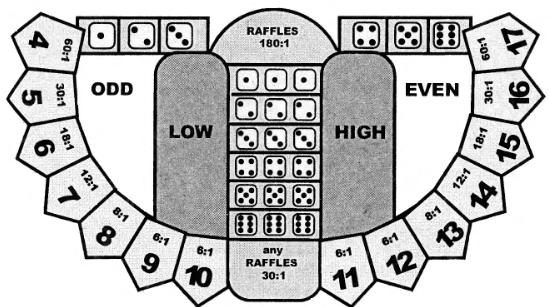
Стол для игры имеет специальную разметку, для того, что-бы игроки могли делать ставки на различный исход при броске трех костей. Положив фишку на любую из 6 комбинаций в поле Raffles, игрок тем самым делает ставку на то, что на всех трех костях одновременно выбросят именно это число очков. В случае удачи его ожидает выигрыш в соотношении 180:1. Поставив на поле Any raffle, игрок выигрывает, если после броска на всех трех костях будет одинаковое число очков, но не важно какое конкретно. Выигрыш выплачивается в соотношении 30:1. На поле Low (мало) выигрывают, когда сумма выпавших очков не более 10. На поле High (много) - когда сумма очков не меньше 11. Выигрыш на Even (чёт) и Odd (нечет) выплачивается в том случае, если выпадает любое четное или соответственно нечетное число. Но если полученное число складывается из трех одинаковых цифр, это означает проигрыш игрока. Кроме этих ставок, есть ставки на конкретную сумму очков, «на числа». На разметке стола видно, в каком соотношении производится выплата выигрыша при ставке на то или иное число. Соотношения разные и зависят от вероятностей выбрасывания каждой суммы.

Не будем повторять расчеты вероятностей для броска трех костей, отмeтим только, что при любой ставке соотношение, выплачиваемое игроку, меньше того, которым оно должно быть исходя из теории. В поле Raffles истинное соотношение равняется 215:1, а значит, казино оставляет себе 16 2/3 % от суммы выигрыша. На каждом поле свой процент, остающийся у казино. Как это посчитать мы наметили в обсуждении предыдущей игры, а вы, при желании можете довести расчеты до конца. Тем самым вооружить себя знаниями, главное из которых - выигрывает всегда казино.

Покер

Для игры необходимо иметь пять игральных костей стандартного вида. Кости бросают из рук или из любого стакана на ровную поверхность. В игре могут участвовать два и более игроков. Цель игры - выполнение определенных фигур с максимальным количеством очков. Первым броском производится жеребьевка очередности хода между игроками. Начинает игрок, набравший наибольшее количество очков, и далее по убыванию очков.

Набор фигур состоит из двух программ: обязательной и произвольной.

Обязательная программа:

единицы, двойки, тройки, четверки, пятерки, шестерки. (Нужно выбросить не менее 3-х костей конкретного достоинства).

Произвольная программа:

• одна пара (1 п) - 2 кости одного достоинства;

• две пары (2п) - 2 кости одного достоинства и 2 кости другого достоинства;

• любая тройка (3) - 3 кости одного достоинства;

• малый стрит (LS) - 5 костей достоинством 1, 2, 3, 4, 5;

• большой стрит (BS) - 5 костей достоинством 2, 3, 4, 5, 6;

• фул (F) - 2 кости одного достоинства и 3 кости другого достоинства;

• каре (С) - 4 кости одного достоинства;

• покер (Р) - 5 костей одного достоинства;

• шанс (Sh) - 5 костей любого достоинства.

Выполнение фигур начинается с обязательной программы. Фигуры произвольной программы можно выполнять только после окончания обязательной программы. Порядок выполнения фигур в программах - произвольный. При каждом ходе игрок имеет право на три попытки для выполнения одной из фигур. После первого броска он оставляет кости, необходимые для задуманной фигуры, а в следующих попытках выбрасывает оставшиеся для получения желаемого результата. При любой из трех попыток можно начинать выполнение другой фигуры в зависимости от ситуации.

Результаты ходов записываются в специальную, заранее расчерченную, таблицу. После выполнения каждого хода обязательной программы могут возникнуть следующие варианты:

1. Выпали 3 кости одного достоинства: тогда в соответствующей клеточке таблицы ставится знак «+», отмечающий выполнение фигуры;

2. Выпало менее 3 костей одного достоинства: в таблицу заносится отрицательный результат, равный числу костей, недостающих до трех, умноженному на их достоинство (при двойках 2, при тройках 3 и т.д.);

3. Выпало более 3 костей одного достоинства: в таблицу записывают положительный результат, равный числу костей сверх трех, умноженному на их достоинство.

 

4. Не выпало ни одной кости нужного достоинства: тогда в таблице указывается отрицательный результат, равный достоинст- вужелаемой кости, умноженному на 3.

Каждый участник может выполнить комбинацию только по одному разу. Например, если у одного из участников вторично выпадает обязательная комбинация «четверки», и возможно с лучшим результатом, то он не может снова занести этот результат в таблицу, а должен выполнять одну из оставшихся комбинаций.

После обязательной программы подводится промежуточный итог. Очки каждого игрока суммируются. Если итог равен нулю или больше, то добавляется премия 50 очков. При выполнении фигуры произвольной программы с первого броска сумма очков её удваивается, кроме шанса. Если при выполнении хода не удалось выбросить нужную фигуру, то по желанию игрока в таблице вычеркиваются очки за любую уже выполненную фигуру. При выполнении покера дается премия 50 очков. Игра заканчивается заполнением всех клеточек таблицы. Очки каждого игрока суммируются, далее производится расчет. Из очков конкретного игрока вычитается среднее арифметическое суммы всех игроков. Положительный результат - это выигрыш, отрицательный - проигрыш. Покажем пример заполнения таблицы с подсчетом очков для одного из игроков и комментариями к процессу игры.

 

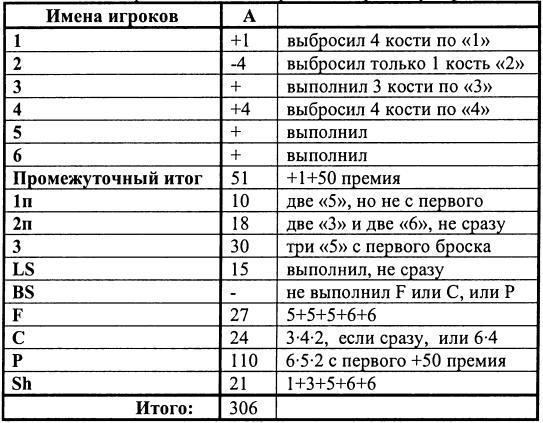
Эта игра представляет собой вариант карточного покера. Причем здесь описан покер с обычными костями, а существуют специальные покерные кости, на гранях которых нанесены карточные символы: девятка, десятка, валет, дама, король и туз.

Итак, мы рассмотрели несколько игр в кости, показали некоторые методы вычислений вероятностей отдельных исходов. Есть еще вариант крэпса для казино со своей разметкой стола, популярная игра пассе ди и множество других. Но покер, как мне кажется, самая интеллектуальная из игр в кости, поэтому на нем закончим разговор об этой группе азартных числовых игр. Игральные кости дали основной толчок для развития комбинаторики и теории вероятностей. А занимались теоретическими исследованиями игр в кости такие великие математики как Тарталья и Галилей, Ферма и Паскаль, оставившие свои имена в науке в связи с другими крупными открытиями и исследованиями.